Tutorials
How to synthesise a refined BT from a set of options
For this tutorial, we will consider a basic graph search problem, where robot actions are navigation actions along edges.
The source code for this tutorial can be found here.
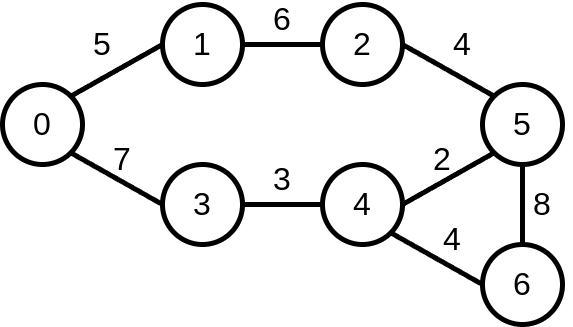
Consider the following undirected graph, where values along edges represent the cost of traversal:
Let’s say that we want to synthesise a BT which navigates the robot to node 5 along the shortest path. For an edge (v,v’), the robot reaches v’ with probability 0.7. The remainder of the probability is uniformly distributed among the other possible successors from v. The expected cost of edge (v,v’) is the weighted average cost according to the edge weights and transition probabilities.
In this tutorial, we will construct an option for each edge action, and use this to synthesise a BT.
We begin by importing all necessary code from refine_plan. We will cover these imports throughout the tutorial.
from refine_plan.algorithms.refine import synthesise_bt_from_options
from refine_plan.models.condition import Label, EqCondition
from refine_plan.models.state_factor import IntStateFactor
from refine_plan.models.option import Option
Our first step in building the options is to define our state space.
We do this by defining a state factor which capture the robot’s current node.
In this instance, the nodes are integers, and so we create an IntStateFactor called node_sf which can take values 0 through 6 inclusive.
# Step 1: Build our state factor for the graph
# The state factor captures the robot's current node
node_sf = IntStateFactor("node_sf", 0, 6)
To define the probabilistic transitions and reward function, we must now capture the connectivity of the above graph. This can be achieved through a nested dictionary:
# Step 2: Define the connectivity of our graph as a dictionary
# graph[v][v'] = cost
graph = {
0: {1: 5, 3: 7},
1: {0: 5, 2: 6},
2: {1: 6, 5: 4},
3: {0: 7, 4: 3},
4: {3: 3, 5: 2, 6: 4},
5: {2: 4, 4: 2, 6: 8},
6: {4: 4, 5: 8},
}
With the graph and our state space defined, we can now compute the probabilistic transitions and
rewards. In refine_plan, we define these using conditions.
For this graph search example, we use EqConditions, or equality conditions. These conditions are
satisfied when a state holds a particular value for a state factor.
With this, we represent probabilistic transitions as a (pre-condition, probabilistic post-conditions) pair. The pre-condition defines the states where this edge/option can be navigated. The probabilistic post-conditions is a dictionary from post-condition to probability. This defines the effects of an edge/option, and the probability of these effects.
We can compute these transitions as follows:
# Step 3: Define our transition function for an edge
# We say that for edge (v,v') there is a 0.7 chance of reaching v
# and a 0.3 chance of that being split evenly across the other possible successor nodes
def trans_probs(src, dst):
"""Compute a (pre_cond, prob_post_conds) pair for a given edge.
pre_cond is the guard for an edge.
prob_post_conds is a dictionary from post conditions to probabilities
Args:
src: The start node of an edge
dst: The destination node of an edge
Returns:
A (pre_cond, prob_post_conds) pair
"""
pre_cond = EqCondition(node_sf, src)
prob_post_conds = {}
for succ in graph[src]:
post_cond = EqCondition(node_sf, succ)
prob = 0.7 if succ == dst else 0.3 / (len(graph[src]) - 1.0)
prob_post_conds[post_cond] = prob
return (pre_cond, prob_post_conds)
The rewards can be computed in a similar way. In refine-plan, rewards for an edge/option are given as a
(pre-condition, reward) pair.
The pre-condition defines when this reward is given.
The reward for an edge can be written as:
# Step 4: Define our reward function for an edge
# Here, we define our reward function to be the expected cost of the edge action
def reward(src, dst):
"""Compute a (pre_cond, reward) pair for a given edge.
pre_cond is the guard for an edge.
reward is the expected cost of an edge
Args:
src: The start node of an edge
dst: The destination node of an edge
Returns:
A (pre_cond, reward) pair
"""
pre_cond = EqCondition(node_sf, src)
reward = 0.0
for succ in graph[src]:
# Get our transition probability again
prob = 0.7 if succ == dst else 0.3 / (len(graph[src]) - 1.0)
edge_weight = graph[src][succ]
# Compute the weighted average
reward += prob * edge_weight
return (pre_cond, reward)
With the transitions and rewards defined, we can now define the options.
Here, we construct an option for each edge the robot can navigate on.
The resulting options are very simple, but can be expanded through more complex transitions and rewards.
An Option requires:
A name, e.g.
e01for the edge between node 0 and 1.A list of transitions, i.e. a list of (pre-condition, probabilistic post-conditions) pairs.
A list of rewards, i.e. a list of (pre-condition, reward) pairs.
We can implement this as follows:
# Step 5: Create an option for each edge
# The options correspond to single robot actions but in practice
# they can capture more complex behaviour
options = []
for src in graph:
for dst in graph[src]:
options.append(
Option(
"e{}{}".format(src, dst), [trans_probs(src, dst)], [reward(src, dst)]
)
)
The final step before synthesising our BT is to define our goal condition for planning.
Here, we want the robot to reach node 5.
We can encode this using labels, which are named conditions.
We can create a Label object which has the name goal and which holds when the robot reaches node 5:
# Step 6: Create our goal label
# The goal label captures reaching node 5
goal = Label("goal", EqCondition(node_sf, 5))
With this, we can now synthesise a BT using synthesise_bt_from_options, which takes:
A list of state factors (only one is required here)
A list of options
A list of labels
An optional initial state. In most problems, this can be set to None
A planning objective specified in the PRISM modelling language. Here we minimise the total reward for the robot to reach the goal state, according to our
goallabel.A default action. Our planner may not synthesise an action for some states, e.g. the goal state. A default action can be provided for these states.
An output file for the BT. The BT is outputted in the XML format used by BehaviorTree.cpp.
# Step 7: Bring everything together and synthesise the refined bt
synthesise_bt_from_options(
[node_sf],
options,
[goal],
initial_state=None,
prism_prop='Rmin=?[F "goal"]',
default_action="idle",
out_file="/tmp/bt.xml",
)
This concludes the tutorial. The BT output by synthesise_bt_from_options cannot be directly executed by BehaviorTree.cpp currently, but should give enough information as to how this could be achieved.
Executable BT XML files will be addressed in the next release.
Learning a set of options represented as dynamic Bayesian networks from data
In the previous tutorial, we assumed that the options for each of the action nodes in the initial BT were known. In this tutorial, we show how to learn these options from simulation data.
The source code for this tutorial can be found within the following script.
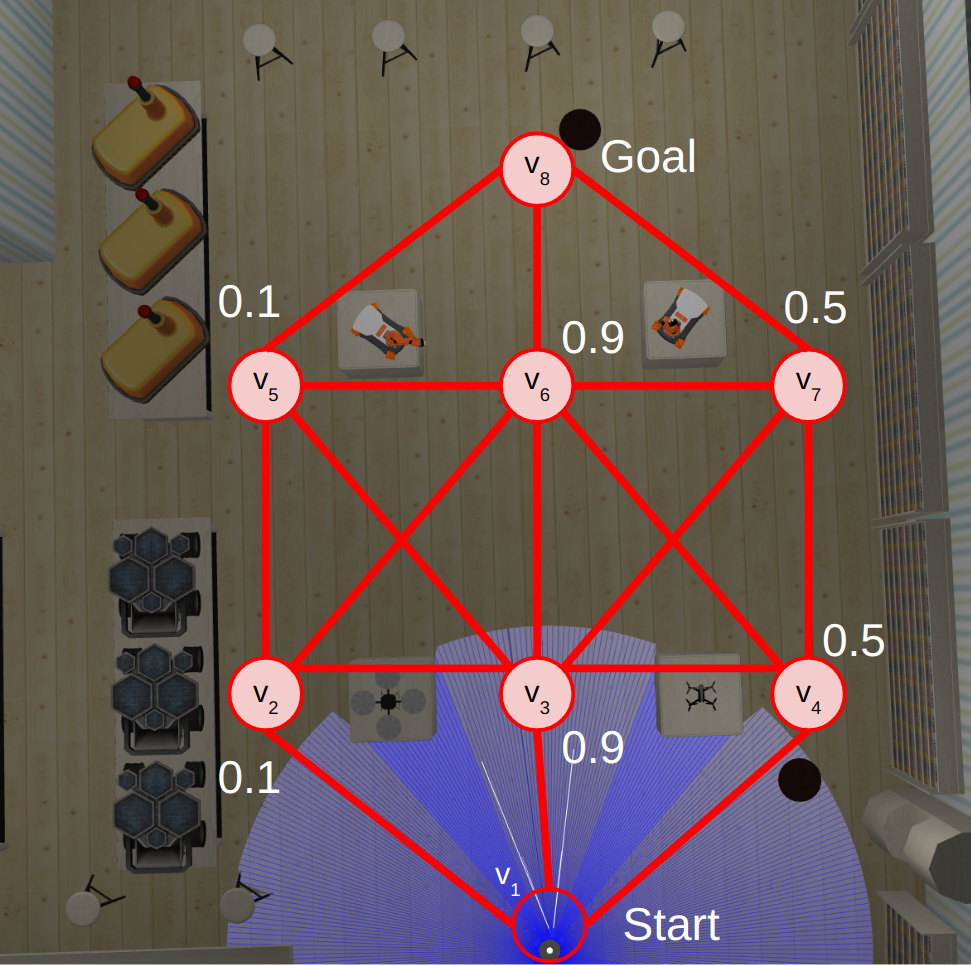
Consider the robot in the robotic museum below:
Here, the robot must navigate from the start to the goal as quickly as possible, where the robot navigates along the edges of a topological map (shown by the red nodes and edges). In the museum, there are doors at nodes v2, v3, v4, v5, v6, and v7. Each of these doors are closed with some probability (as shown above). The robot can check whether a door is open when it reaches it. If the door is closed, the robot may open it, however, this takes 30 seconds.
In this tutorial, we will construct a set of options for the edge navigation, door checking, and door opening actions.
We begin by importing all necessary code from refine_plan.
We will cover these imports throughout the tutorial.
from refine_plan.models.condition import Label, EqCondition, AndCondition, OrCondition
from refine_plan.learning.option_learning import mongodb_to_yaml, learn_dbns
from refine_plan.models.state_factor import StateFactor
from refine_plan.models.dbn_option import DBNOption
from refine_plan.models.state import State
Our first step for option learning is to define the state space that the options operate over.
In future releases of REFINE-PLAN this will be extracted automatically, however in the current release it must be specified manually.
We do this by defining a state factor which capture the robot’s current node, and a state factor capturing the status of each door, which can be unknown, closed, or open.
These state factors all use string values, and can be represented with the StateFactor class:
loc_sf = StateFactor("location", ["v{}".format(i) for i in range(1, 9)])
door_sfs = [
StateFactor("v2_door", ["unknown", "closed", "open"]),
StateFactor("v3_door", ["unknown", "closed", "open"]),
StateFactor("v4_door", ["unknown", "closed", "open"]),
StateFactor("v5_door", ["unknown", "closed", "open"]),
StateFactor("v6_door", ["unknown", "closed", "open"]),
StateFactor("v7_door", ["unknown", "closed", "open"]),
]
Next, we define the connectivity of the topological map, and the edges which are potentially blocked by doors. This can be achieved through a number of dictionaries:
GRAPH = {
"v1": {"e12": "v2", "e13": "v3", "e14": "v4"},
"v2": {"e12": "v1", "e23": "v3", "e25": "v5", "e26": "v6"},
"v3": {
"e13": "v1",
"e23": "v2",
"e34": "v4",
"e35": "v5",
"e36": "v6",
"e37": "v7",
},
"v4": {"e14": "v1", "e34": "v3", "e46": "v6", "e47": "v7"},
"v5": {"e25": "v2", "e35": "v3", "e56": "v6", "e58": "v8"},
"v6": {
"e26": "v2",
"e36": "v3",
"e46": "v4",
"e56": "v5",
"e67": "v7",
"e68": "v8",
},
"v7": {
"e37": "v3",
"e47": "v4",
"e67": "v6",
"e78": "v8",
},
"v8": {"e58": "v5", "e68": "v6", "e78": "v7"},
}
CORRESPONDING_DOOR = {
"e12": None,
"e14": None,
"e58": "v5",
"e78": "v7",
"e13": None,
"e36": "v3",
"e68": "v6",
"e25": "v2",
"e47": "v4",
"e26": "v2",
"e35": "v3",
"e46": "v4",
"e37": "v3",
"e23": None,
"e34": None,
"e56": None,
"e67": None,
}
With this, we now move onto option learning. This tutorial assumes you have access to a MongoDB instance with simulation data for each action the robot may execute. Individual data items should have the following format:
{
_id: ObjectId('670ff634a4d98a85eee1487d'),
run_id: 502334331,
option: "e12",
duration: 15.007,
location0: "v1",
v2_door0: "unknown",
v3_door0: "unknown",
v4_door0: "unknown",
v5_door0: "unknown",
v6_door0: "unknown",
v7_door0: "unknown",
locationt: "v2",
v2_doort: "unknown",
v3_doort: "unknown",
v4_doort: "unknown",
v5_doort: "unknown",
v6_doort: "unknown",
v7_doort: "unknown"
}
Here, _id represents the document ID; run_id is an identifier for the simulation run; option is the option/action being executed;
duration is the execution duration (corresponding to the reward/cost in this instance); location0(t) represents the robot’s starting (finishing) location; and
vi_door0(t) represents the door status of vi before (after) executing the option.
Given the Mongo database, we convert it into a YAML file for learning:
mongodb_to_yaml(
mongo_connection_str,
"refine-plan",
"fake-museum-data",
[loc_sf] + door_sfs,
"../data/fake_museum/dataset.yaml",
)
In mongodb_to_yaml we require a MongoDB connection string, e.g. localhost:27017.
The second and third arguments refer to the database and collection name on the MongoDB instance, respectively.
The fourth argument is the list of state factors, and the fifth is a path to output the dataset to.
After writing the YAML dataset, we can learn dynamic Bayesian networks (DBNs) for the transition and reward (which corresponds to time in this example) functions for each option:
dataset_path = "../data/fake_museum/dataset.yaml"
output_dir = "../data/fake_museum/"
learn_dbns(dataset_path, output_dir, [loc_sf] + door_sfs)
The learn_dbns function requires the YAML dataset, an output directory, and the list of state factors.
Given the DBNs for each option, we now need to collect them into DBNOption objects.
The DBNOption constructor requires a Condition object which describes the states in which this option can be executed.
For the museum navigation problem we provide the function below, which captures edge connectivity and the effects of doors on navigation:
def _get_enabled_cond(sf_list, option):
"""Get the enabled condition for an option.
Args:
sf_list: The list of state factors
option: The option we want the condition for
Returns:
The enabled condition for the option
"""
sf_dict = {sf.get_name(): sf for sf in sf_list}
door_locs = ["v{}".format(i) for i in range(2, 8)]
if option == "check_door" or option == "open_door":
enabled_cond = OrCondition()
door_status = "unknown" if option == "check_door" else "closed"
for door in door_locs:
enabled_cond.add_cond(
AndCondition(
EqCondition(sf_dict["location"], door),
EqCondition(sf_dict["{}_door".format(door)], door_status),
)
)
return enabled_cond
else: # edge navigation option
enabled_cond = OrCondition()
for node in GRAPH:
if option in GRAPH[node]:
enabled_cond.add_cond(EqCondition(sf_dict["location"], node))
door = CORRESPONDING_DOOR[option]
if door != None:
enabled_cond = AndCondition(
enabled_cond, EqCondition(sf_dict["{}_door".format(door)], "open")
)
return enabled_cond
Given the enabled conditions for each option, we now create a series of DBNOption objects, one for each option.
The DBNOption requires the name of the option, the file path for the transition and reward DBNs, the list of state factors, and the enabled condition:
sf_list = [loc_sf] + door_sfs
option_names = [
"e12",
"e14",
"e58",
"e78",
"e13",
"e36",
"e68",
"e25",
"e47",
"e26",
"e35",
"e46",
"e37",
"e23",
"e34",
"e56",
"e67",
"check_door",
"open_door",
]
option_list = []
for option in option_names:
print("Reading in option: {}".format(option))
t_path = "../data/fake_museum/{}_transition.bifxml".format(option)
r_path = "../data/fake_museum/{}_reward.bifxml".format(option)
option_list.append(
DBNOption(
option, t_path, r_path, sf_list, _get_enabled_cond(sf_list, option)
)
)
We now have a set of DBNOptions learned from data which capture the transition and reward dynamics for a set of robot actions.
This concludes the tutorial on how to learn a set of options from simulation data.
But we can go one step further. given the option_list above, we can now synthesise the refined BT similar to the previous tutorial.
Recall that the robot must minimise the expected time to reach the goal.
To plan using our learned options, we first define our initial state, which captures the robot at node v1 with no knowledge of the doors.
We then define a goal condition which is satisfied when the robot reaches node v8.
We then call synthesise_bt_from_options as in the previous tutorial:
# Define the initial state
init_state_dict = {sf: "unknown" for sf in door_sfs}
init_state_dict[loc_sf] = "v1"
init_state = State(init_state_dict)
# Add a goal label
labels = [Label("goal", EqCondition(loc_sf, "v8"))]
synthesise_bt_from_options(
sf_list,
option_list,
labels,
initial_state=init_state,
prism_prop='Rmin=?[F "goal"]',
default_action="idle",
out_file="/tmp/bt.xml",
)
This concludes the extended version of this tutorial.
Note that the BT output by synthesise_bt_from_options cannot currently be directly executed by BehaviorTree.cpp.
This will be addressed in the next release.
Planning an exploration policy to support Bayesian network learning
In this tutorial, we show how to efficiently collect data to support Bayesian network learning. For this, we implement the active exploration approach MAX. The above tutorials should be followed prior to this one.
The source code for this tutorial can be found in the following script.
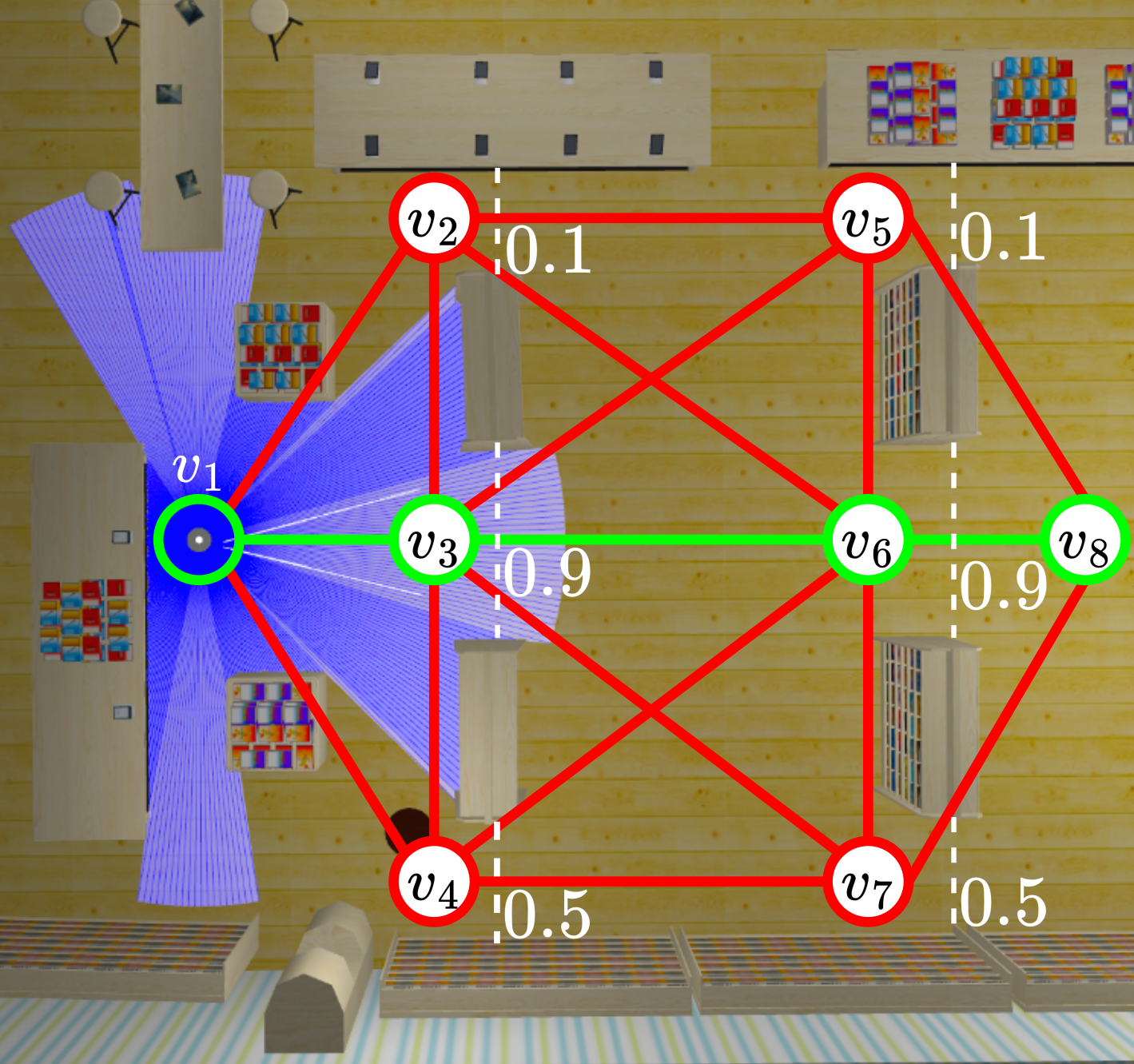
Consider the robot in the bookstore below:
Here, the robot must navigate from the start to the goal as quickly as possible, where the robot navigates along the edges of a topological map (shown by the red nodes and edges). In the bookstore, there are doors at nodes v2, v3, v4, v5, v6, and v7. Each of these doors are closed with some probability (as shown above). The robot can check whether a door is open when it reaches it. If the door is closed, the robot may open it, however, this takes 30 seconds.
In this tutorial, we will synthesise an exploration policy which executes actions the robot knows less about.
We begin by importing all necessary code from refine_plan.
We will cover these imports throughout the tutorial.
from refine_plan.models.condition import EqCondition, AndCondition, OrCondition
from refine_plan.algorithms.explore import synthesise_exploration_policy
from refine_plan.models.state_factor import StateFactor
from refine_plan.models.state import State
import sys
First, we define the connectivity of the topological map, and the edges which are potentially blocked by doors. This can be achieved through a number of dictionaries. We also define the robot’s start and end location.
GRAPH = {
"v1": {"e12": "v2", "e13": "v3", "e14": "v4"},
"v2": {"e12": "v1", "e23": "v3", "e25": "v5", "e26": "v6"},
"v3": {
"e13": "v1",
"e23": "v2",
"e34": "v4",
"e35": "v5",
"e36": "v6",
"e37": "v7",
},
"v4": {"e14": "v1", "e34": "v3", "e46": "v6", "e47": "v7"},
"v5": {"e25": "v2", "e35": "v3", "e56": "v6", "e58": "v8"},
"v6": {
"e26": "v2",
"e36": "v3",
"e46": "v4",
"e56": "v5",
"e67": "v7",
"e68": "v8",
},
"v7": {
"e37": "v3",
"e47": "v4",
"e67": "v6",
"e78": "v8",
},
"v8": {"e58": "v5", "e68": "v6", "e78": "v7"},
}
CORRESPONDING_DOOR = {
"e12": None,
"e14": None,
"e58": "v5",
"e78": "v7",
"e13": None,
"e36": "v3",
"e68": "v6",
"e25": "v2",
"e47": "v4",
"e26": "v2",
"e35": "v3",
"e46": "v4",
"e37": "v3",
"e23": None,
"e34": None,
"e56": None,
"e67": None,
}
# Problem Setup
INITIAL_LOC = "v1"
GOAL_LOC = "v8"
To support policy synthesis, we now create a function _get_enabled_cond which captures the states in which each action is enabled.
This function reasons over edge connectivity and the effects of doors on navigation.
def _get_enabled_cond(sf_list, option):
"""Get the enabled condition for an option.
Args:
sf_list: The list of state factors
option: The option we want the condition for
Returns:
The enabled condition for the option
"""
sf_dict = {sf.get_name(): sf for sf in sf_list}
door_locs = ["v{}".format(i) for i in range(2, 8)]
if option == "check_door" or option == "open_door":
enabled_cond = OrCondition()
door_status = "unknown" if option == "check_door" else "closed"
for door in door_locs:
enabled_cond.add_cond(
AndCondition(
EqCondition(sf_dict["location"], door),
EqCondition(sf_dict["{}_door".format(door)], door_status),
)
)
return enabled_cond
else: # edge navigation option
enabled_cond = OrCondition()
for node in GRAPH:
if option in GRAPH[node]:
enabled_cond.add_cond(EqCondition(sf_dict["location"], node))
door = CORRESPONDING_DOOR[option]
if door != None:
enabled_cond = AndCondition(
enabled_cond, EqCondition(sf_dict["{}_door".format(door)], "open")
)
return enabled_cond
With this, we now define the planning problem for exploration.
We begin by defining state factors which capture the robot’s current node, and a state factor capturing the status of each door, which can be unknown, closed, or open.
These state factors all use string values, and can be represented with the StateFactor class:
loc_sf = StateFactor("location", ["v{}".format(i) for i in range(1, 9)])
door_sfs = [
StateFactor("v2_door", ["unknown", "closed", "open"]),
StateFactor("v3_door", ["unknown", "closed", "open"]),
StateFactor("v4_door", ["unknown", "closed", "open"]),
StateFactor("v5_door", ["unknown", "closed", "open"]),
StateFactor("v6_door", ["unknown", "closed", "open"]),
StateFactor("v7_door", ["unknown", "closed", "open"]),
]
sf_list = [loc_sf] + door_sfs
Next, we list all of the action nodes the robot can execute, and compute the enabled condition for each action.
action_names = [
"e12",
"e14",
"e58",
"e78",
"e13",
"e36",
"e68",
"e25",
"e47",
"e26",
"e35",
"e46",
"e37",
"e23",
"e34",
"e56",
"e67",
"check_door",
"open_door",
]
enabled_conds = {}
for act in action_names:
enabled_conds[act] = _get_enabled_cond(sf_list, act)
Finally, we create our initial State for the robot and call synthesise_exploration_policy.
synthesise_exploration_policy takes a connection string, database, and collection name for a MongoDB instance.
This is for reading existing data collected for the model.
Next it receives the StateFactor objects and a list of action node names.
After that it receives a parameter describing the size of the ensemble models used for MAX.
We recommend a value less than or equal to 10.
After that, the exploration episode length is passed in.
The last two parameters are the enabled conditions for each action node and the robot’s initial state.
init_state_dict = {sf: "unknown" for sf in door_sfs}
init_state_dict[loc_sf] = "v1"
init_state = State(init_state_dict)
policy = synthesise_exploration_policy(
connection_str,
"refine-plan",
"bookstore-data",
sf_list,
action_names,
10,
100,
enabled_conds,
initial_state=init_state,
)
In this example, BT action nodes are treated as black boxes.
To support geometric reasoning, a user may wish to parametrise the behaviour within each action node.
This is supported through the use of motion parameters.
For this, synthesise_exploration_policy has an additional optional parameter called motion_params, which maps from action names to a list of parameters for that action.
For example, if we have a robot manipulator that can pick up objects with different grasps, the motion_params dictionary may look like:
motion_params = {"pick_up": ["top", "left", "right", "up", "down"]}
This captures all possible directions the robot could grasp an object from. When motion parameters are provided, the data for each action will be split by motion parameter in the MongoDB database.